Posts Tagged ‘algebra’

Brief note: a time-out from art-related items to post an assignment for a Coursera class for assessment by peers.

Unit: Exponential Relationships

click for link to image

9th grade, but 8th graders are welcome!

Investigation 1: Exponential Growth

Welcome to our new unit in Connected Math, Exponential Relationships! We have five different investigations, and you will find yourself doing a lot of comparisons of exponential relationships with linear relationships. (Told you linear would never go away!) You can see an overview of the unit by clicking on the link above to see the parent information letter. DO NOT WAIT TO GET YOUR NEW UNIT BOOK from your district office – you don’t want to get behind!!

Here are two key pieces we will focus on:

• * Is the relationship between variables an example of exponential growth or decay? Why?
• • How can this relationship be detected in a table, graph, or equation? What is the growth factor?
• • What table, graph, or equation would model the data or the pattern in a graph relating the variables?
• • How could I answer questions about an exponential situation by studying a table, a graph, or an equation of the exponential relationship?
• • How does this exponential relationship compare to other relationships between variables I have studied?

(All of the above from Connected Math 2: Growing, Growing, Growing)

Stuck? Email: ***************@***************

Now to the fun stuff: Investigation 1

• You will need: scissors and a sheet of paper (regular paper is fine, and you might be happier with a blank sheet)
• Your journal for record-keeping, notes, and solving problems
• A new anchor chart for vocabulary on a separate page in your journal – use a stickie tab on the page for easy reference to it.
• [Reference for peer readers on anchor charts – http://www.julieballew.com/A_Literate_Life/Photos/Pages/Anchor_Charts.html. Students will have other samples, since what I use I cannot share publicly (only in a classroom/online teaching setting) because of proprietary agreement with past employer)].

(Students have experience with anchor charts, and throughout the online lessons, I will have links to the unit anchor charts.)

1. Read on page 5, 1.1 Making Ballots and complete the short experiment.

2. Answer questions in your journal from page 6. Remember to indicate the investigation, number of the problem, and use complete sentences!

3. Upload your problem to the dropbox by ____________ for feedback from Mrs. Moran. (This should take no more than 1 day.)

4. Begin working on homework problems for this investigation: Practice problems on page 11 – 18: Everyone do #1-14, and then 3 others of your choice. Everyone do #33 – 38. (Due at the end of the week.)

Stuck? Email: ***************@***************

5. Read on page 6, 1.2 Requesting a Reward and add the new vocabulary to your anchor chart for this unit.

6. Complete the “Getting Ready” on page 6 in your journal.

7. Complete problem 1.2 on page 7 in your journal. Remember to indicate the investigation, number of the problem, and use complete sentences!

8. Upload your problem to the dropbox by ____________ for feedback from Mrs. Moran. (This should take no more than 1 day.)

9. Continue working on homework problems for this investigation: Practice problems on page 11 – 18: Everyone do #1-14, and then 3 others of your choice. Everyone do #33 – 38. (Due at the end of the week.)

Stuck? Email: ***************@***************

10. Read on page 8, 1.3 Making a New Offer and add the new vocabulary to your anchor chart for this unit.

11. Answer questions from page 9 in your journal.  Remember to indicate the investigation, number of the problem, and use complete sentences!

12. Upload your problem to the dropbox by ____________ for feedback from Mrs. Moran. (This should take no more than o1 day.)

13. Check out this video and try experimenting with values. Think about what you notice and try and make a connection between the video and the investigation.

Stuck? Email: ***************@***************

 

14. Continue working on homework problems for this investigation: Practice problems on page 11 – 18: Everyone do #1-14, and then 3 others of your choice. Everyone do #33 – 38. (Due at the end of the week.)

15. Log onto the class discussion forum (*******************address) and complete two responses. a) What are you discovering so far about exponential growth? and b) what differences do you notice between linear and exponential growth? (Due by the end of the week.) (Rubric http://www.mtsu.edu/ltanditc/docs/Discussion_Board_Rubrics.pdf)

16. Check out this video and see about exponential growth in real-world examples. You might get a few ideas for your Mathematical Reflection.

17. Start your draft of your mathematical reflection on page 19.

18. Read page 10, 1.4 Getting Costs in Line.

19. Answer questions from page 10 in your journal.  Remember to indicate the investigation, number of the problem, and use complete sentences!

20. Upload your problem to the dropbox by ____________ for feedback from Mrs. Moran. (This should take no more than 1 day.)

21. Upload your homework problems to the dropbox by ___________ for feedback from Mrs. Moran. (Due end of the week.)

Extra video – if you want to dig a little deeper and are interested in growth in businesses –

22. Complete your mathematical reflection on page 19. Use your word processor to complete the assignment. Use complete sentences – FOLLOW THE RUBRIC you already use for these! This is due by the end of the week – allow yourself two days for draft and final copy.

23. Breath Deeply and congratulations! You’ve made a major start in understanding a very practical application of algebra!!!!

Deadlines:

Investigation 1.1 should be completed within a day.

Investigation 1.2 should be completed within a day

Investigation 1.3 should be completed within a day.

Investigation 1.4 should be completed within a day.

Homework Problems due  end of the first week.

Discussion forum responses due the end of the first week.

Mathematical Reflection due the end of the first week.

STATE STANDARDS:

• HS.F-LE.A.1a. Distinguish between situations that can be modeled with linear functions and with exponential functions.
• HS.F-LE.A.1b. Prove that linear functions grow by equal differences over equal intervals, and that exponential functions grow by equal factors over equal intervals.

Mathematical Practice Standards:

• 1. Make sense of problems and persevere in solving them.
• 2. Reason abstractly and quantitatively.
• 3. Construct viable arguments and critique the reasoning of others.
• 4.Model with mathematics.
• 5.Use appropriate tools strategically.
• 6.Attend to precision.
• 7.Look for and make use of structure.
• 8.Look for and express regularity in repeated reasoning.

Copyright notice: all links are public domain and links are included by clicking on pictures. This unit is directly from Connected Math 2, published by Pearson. The conversion to an online format is the work of the instructor, Linda Moran, and cannot be reproduced without permission of the instructor.

SO….I was awake early morning composing the start to this small rant. Yesterday a former retired colleague posted that he, the art teacher,  had subbed for a math teacher and within five minutes had convinced all the students that algebra was pointless in their lives. My quick Facebook comment was something like “oh, so NOT true….”

As I pondered this during the night, I thought of a bunch of things. That math teacher who has struggled all year trying to convince most of the students that algebra is worthwhile just had his job made so much harder. If a math teacher subbed in an art teacher’s classroom and said “why do art because it’ll never make you any money,” he/she has effectively destroyed a lot of budding artists.

Kids listen to what adults say. Now I’m coming at this rant from both angles. I teach college algebra one morning a week at The Art Institute of Tucson. Art and Math, so there. I really work at developing mathematical examples that are applicable to adult students, many of whom see no point to college algebra. So let’s take a look at the practical applications of algebra and all its rules in real life.

1. Order of operations (PEMDAS): if you’re an artist, you don’t pick out your matting before the painting is done. If you’re a chef, you know certain recipes HAVE to be done in a certain order or you ruin the dish. In real life you don’t put your underwear on last. Life is governed by some basics, and that’s what order of operations is all about. This principle teaches you to look for and use order. If you’re designing a video game or a movie, a story board is pretty darn important. Some things have to happen first before others.

2. Algebra teaches you to think: boy, do students hate this one, but it’s true. There is order in life, and algebra is an exercise that gets us to see what we have to do first, second, and so on. Solving equations is all about thinking through the problem and following a set of steps. Reading directions is much the same (even if you’re like my hubby and try to intuit what comes first….)  Laying out a sewing pattern for cutting is thoughtful. If you think of a menu for an event as an equation, you realize that you have to proceed through the preparation pretty thoughtfully.

3. Combining like terms: think about recipes and ordering. One recipe calls for three cups of flour, another for 2 cups of flour, and the third one just a couple of tablespoons. Do you order each separately? Hopefully not, because that would be tedious and time consuming and probably not cost effective. That’s what combining like terms is all about. 3A + 5B + 2C = 240 could be  your supply order and total amount for an event, an art project. Think about planning your art budget for the year for your classroom. You are ordering construction paper….you break it down to amount of packages of each color needed, and then you end up combining all the construction paper before going on to think about your paints. Then you total everything for the final amount. Combining like terms….

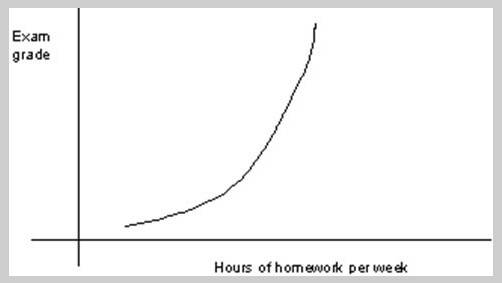
4. Exponential functions: recognizing these functions is pretty darn important if you are buying a car, a house, or medicine, just to name a few.

http://www.ehow.com/info_8145457_jobs-use-exponents.html

You better hope your pharmacist understands how long certain meds stay in your bloodstream before you have to take a new dose. Or…do you understand just how much you are paying in a car loan per month (which is linear) and how the time of your loan affects the value of your car (exponential). And if you want to win the big lottery……

5. Quadratic functions: aside from the fact that the makers of Angry Birds are making a small fortune using quadratic functions to create a game, anyone who has done anything in sports will recognize that a golf swing, a basketball shot, a baseball swing, a forward pass with recognize the inevitable parabola created.

http://www.mathamazement.com/Lessons/Pre-Calculus/02_Polynomial-and-Rational-Functions/quadratic-functions.html

You better hope your professional sports coach understands the equations that will improve your abilities.

So just a few examples……I could go on, but hopefully I’ve made a convert or two. And…just because…here’s a classic Abbot and Costello routine to show just how easily math can be misunderstood…..

May the Algebra Force be with you……….

Today was the first day of two for professional development on Understanding by Design, or UbD. The staff at the school all has to have this training as part of our three-year plan, and I was resisting this because I’ve read through elements of this on my own, as well as tried to apply some of the “big ideas” to a museum project several years ago. I am here to say today is causing me to seriously rethink retirement – the day was amazing, and I do not say that lightly about professional development.

Understanding by Design is a three-stage program to develop more meaningful curriculum that is effective, engages students, and promotes enduring understanding, as Howard Gardner would say. We spent the day on Stage 1, unwrapping the curriculum in order to plan for the end result. Duh. In 20 years of doing student theater, I always did what I call “backplanning,” but NOT ONCE did I think to apply that skill to my classroom teaching.

As we continued through the day, I kept seeing lights at the end of the tunnel, answering for me ways to fix what I am unhappy with in my algebra classes. I do too much direct instruction, I don’t have the kids do enough inquiry, and they aren’t engaged enough or see algebra as a meaningful course of study. I actually wanted to read through standards and try to cluster some of the performance objectives so the planning  makes more sense. The warm-up we did would make more sense than the (to be honest) drill and kill I usually do for practice (and, really honest, management…). In fact, I have some ideas for small group bell work for next week to extend some of the understanding.

All through the day I was (and still am) very conflicted. I am planning to retire in two and a half more years. I have been dealing with some health issues that may make me retire early. Plus, I realized if I go the full years more I will actually end up hurting my retirement benefits, as there hasn’t been a raise, and nothing is in sight. Two and a half years would cut off one of my higher salary years. So I am looking at numbers.

But then I sit in a workshop and get truly excited about trying some new strategies and ideas for teaching algebra, and I don’t want to leave. Retirement is an ending, as well as a beginning. I started teaching 40 years ago this September, and while it is probably time – age-wise – to go, it feels like “the end.” I don’t think I’m ready for closure, even though I want to seriously expand my art work and licensing. I’m not sure I can “let go” of 33 years of teaching, when I still feel like I have a lot more to offer. I still love this stuff – workshops, class management, curriculum, and all. I miss the teaching teachers that I used to do. I have all these skills and experiences (and endorsements) from all these years, and I’m not sure I can give it up…..

So just when I think I am coming to decisions, something happens to change it all. Darn you, Dr. Larry….now what do I do?